Binary Tree

Introduction

Binary trees are used to quickly insert, search and delete data. The following sections present how insert and delete operations are implemented in Never programming language.

record Node
{
    value : int;
    left : Node;
    right : Node;
}

Each node in binary tree consists of value and left and right subtrees.

Insert

func btree_insert(tree : Node, value : int) -> Node
{
    if (tree == nil)
    {
        Node(value, nil, nil)
    }
    else if (value < tree.value)
    {
        tree.left = btree_insert(tree.left, value);
        tree
    }
    else if (value >= tree.value)
    {
        tree.right = btree_insert(tree.right, value);
        tree
    }
    else
    {
        Node
    }
}

Insert operation is very simple. If value being inserted is less than node's value then value is inserted in left subtree. When value is larger or equal node's value then value is inserted in right subtree.

func main() -> int
{
    var btree = Node;

    btree = btree_insert(btree, 10);
    btree = btree_insert(btree, 5);
    btree = btree_insert(btree, 20);
    btree = btree_insert(btree, 1);
    btree = btree_insert(btree, 12);
    btree = btree_insert(btree, 25);
    btree_print(btree, 0);

    0
}

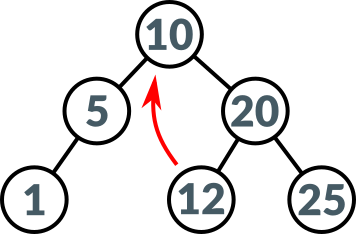
The above code snippet presents how binary tree shown in the above picture is created.

Delete

func btree_min(tree : Node) -> Node
{
    var min = Node;

    min = tree;
    while (min != nil && min.left != nil)
    {
        min = min.left
    };

    min
}

func btree_delete(tree : Node, value : int) -> Node
{
    if (tree != nil)
    {
        if (value < tree.value)
        {
            tree.left = btree_delete(tree.left, value);
            tree
        }
        else if (value > tree.value)
        {
            tree.right = btree_delete(tree.right, value);
            tree
        }
        else
        {
            if (tree.left == nil && tree.right == nil)
            {
                Node
            }
            else if (tree.left == nil)
            {
                tree.right
            }
            else if (tree.right == nil)
            {
                tree.left
            }
            else
            {
                tree.value = btree_min(tree.right).value;
                tree.right = btree_delete(tree.right, tree.value);
                tree
            }
        }
    }
    else
    {
        Node(value, nil, nil)
    }
}

Delete operation is executed in the following three cases:

1. Delete node with no subtrees (left and right are nil).
2. Delete node with one subtree (left xor right is nil).
3. Delete node with both subrees (left and right are not nil).

First two cases are very simple. When node contains no subtrees (is a leaf) then it can be safely deleted (case 1.). Also when node contains only one subtree then such node is deleted and deleted node's parent will point to only subtree (case 2). Case 3. is a little bit more complicated. In this implementation it was decided to search for inorder successor of deleted node. Inorder successor can be found by searching minimum value of the right subtree. Function btree_min returns inorder successor. After its value is replaced in current node, then it is deleted as inorder successor is a leaf.

func main() -> int
{
    btree = btree_delete(btree, 10);
    btree_print(btree, 0);

    0
}

}

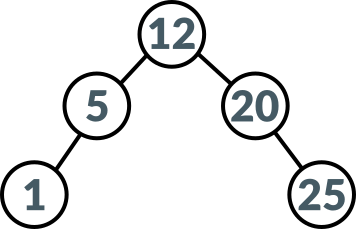
Binary tree which is used as an example in this article, after node 10 is deleted is shown above.

Print

func btree_print(tree : Node, depth : int) -> string
{
    if (tree != nil)
    {
        if (tree.left != nil)
        {
            btree_print(tree.left, depth + 1)
        }
        else
        {
            prints("nil\n")
        };

        prints("value = " + tree.value + " at depth " + depth + "\n");

        if (tree.right != nil)
        {
            btree_print(tree.right, depth + 1)
        }
        else
        {
            prints("nil\n")
        }
    }
    else
    {
        prints("nil\n")
    }
}

There are many ways to print out binary tree. The above function presents binary tree in order representation.

Summary

This short article presents how basic binary tree can be implemented in Never programming language. Search operation is left unspecified as an exercise.