Neural Network in Never
Introduction
Never is a functional programming language which includes matrices as first class objects. It is very likely that you hear about Never for the first time. I will demonstrate its major functions by implementing a simple neural network. In fact it is an example of neural network basic component known as perceptron. I will try to explain everything step by step so you can follow the article easily.
Sigmoid
func sigmoid(x : float) -> float
{
1.0 / (1.0 + exp(-x))
}
Almost all programming languages include a concept of a function. In the above
example function sigmoid takes x as formal parameter and
returns function value. The function transforms almost all values below zero
to zero and almost all values above zero to one. It is used in neural networks
to have zero-one results for parameters.
Linear Congruential Generator
func randomize(seed : int) -> () -> int
{
let v = seed;
func rand() -> int
{
v = (v * 1103515245 + 12345) % 2147483648
}
rand
}
Functions in Never can be nested to any level. They can also access parameters
or local variables defined in their syntactic scope. In the above
example function rand can access and modify variable v defined
in the scope of function randomize. Each time the function is invoked
variable v will be modified and can be treated as local counter.
Functions are also first class objects which means they can be accepted
or returned by other functions. In the above example function rand
is returned by function randomize. What is also noticeable is that
v becomes closed in the scope of function returned. Because of that
sometimes functions such as rand are called closures.
In particular function rand is a linear congruential generator or in simple
words a function which generates pseud-random values. It will be used later
to initialize neural network.
Matrix Algebra
func print_matrix(W[D1, D2] : float) -> int
{
let r = 0;
for (r = 0; r < D1; r = r + 1)
{
let c = 0;
for (c = 0; c < D2; c = c + 1)
{
prints(W[r, c] + " ")
};
prints("\n")
}
}
Never supports matrices which can be passed and returned by functions as any
other type. In the above example function print_matrix takes two dimensional
array W as its formal parameter. Function dimensions are accessible
by parameters D1 and D2. Such matrix passing style is known as
conformant arrays and lets to avoid problems of accessing matrces elements out
of their bounds. The above function prints matrix elements in row order. First
all elements in columns of row 0, next of row 1, and so on. Function prints
takes string as parameter and prints it on console. Addition operator is overloaded
(which means it can take arguments of different types) and in the above case adds
float and string parameter by changing float into its string representation.
func one_matrix(W[D1, D2] : float) -> int
{
let r = 0;
for (r = 0; r < D1; r = r + 1)
{
let c = 0;
for (c = 0; c < D2; c = c + 1)
{
W[r, c] = 1.0
}
}
}
Functions can also modify passed parameters. The above function initializes all matrix elements to one. Later this matrix will be used to perform matrix subtraction.
func rand_matrix(W[D1, D2] : float, rand() -> int) -> int
{
let r = 0;
for (r = 0; r < D1; r = r + 1)
{
let c = 0;
for (c = 0; c < D2; c = c + 1)
{
W[r, c] = (rand() % 1000) / 1000.0
}
}
}
func sigmoid_matrix(W[D1, D2] : float) -> [_,_] : float
{
let S = {[ D1, D2 ]} : float;
let r = 0;
for (r = 0; r < D1; r = r + 1)
{
let c = 0;
for (c = 0; c < D2; c = c + 1)
{
S[r, c] = sigmoid(W[r, c])
}
};
S
}
Of course we may initialize matrix elements to any value. Function rand_matrix
assigns values generated by function rand to matrix elements. The example
also presents how function rand is passed as a parameter. Second example
shows how function sigmoid_matrix calculates sigmoid values for each
matrix elements.
func T_matrix(W[D1, D2] : float) -> [_,_] : float
{
let T = {[ D2, D1 ]} : float;
let r = 0;
for (r = 0; r < D1; r = r + 1)
{
let c = 0;
for (c = 0; c < D2; c = c + 1)
{
T[c, r] = W[r, c]
}
};
T
}
One of common matrix operation is transposition. The function T_matrix
returns matrix whose element at index [r, c] is placed at index [c, r]
in the returned matrix.
func Hadamard_matrix(W1[D1, D2] : float, W2[D3, D4] : float) -> [_,_] : float
{
let H = {[ D1, D2 ]} : float;
let r = 0;
for (r = 0; r < D1; r = r + 1)
{
let c = 0;
for (c = 0; c < D2; c = c + 1)
{
H[r, c] = W1[r, c] * W2[r, c]
}
};
H
}
Matrices can also be multiplied. Hadamard multiplication is a special kind
of multiplication where each element of matrix W1 is multiplied
by corresponding element of matrix W2. Of course each matrix should
have same dimensions size. Matrix multiplication which uses dot product
to calculate values of its elements is implemented in Never by operator *.
As all basic building operations are described we can implement neural network.
Forward Propagation
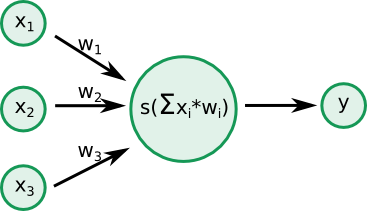
Supervised learning is one of methods used to generate neural network. The algorithm has set of inputs and set of expected results. The difference between expected result and output generated by the network is used to change neural network parameters. The algorithm may be formalized in matrix algebra.
As usual lets start with basic components which are needed. As stated above
we need set of inputs x and expected results y. They may be
expressed in Never as follows:
let x = [ [0, 1, 0],
[1, 0, 0],
[1, 1, 1],
[0, 0, 1] ] : float;
let y = [ [1, 0, 1, 0] ] : float;
let yT = T_matrix(y);
Expected results y are single values. To simplify notation instead of typing
y = [ [1], [0], [1], [0] ] it is more convenient to define vector
y = [ 1, 0, 1, 0 ] and transpose it. As you may notice it is expected
the the network will ignore boundary values x0, x2 and
return only value of x1.
Input weights W are first initialized to random values. The following code
can set [3, 1] matrix.
let W = {[ 3, 1 ]} : float;
let rand = randomize(165);
rand_matrix(W, rand);
Now output calculation formula is simple. What is also worth noticing is that
array s contains four values for each input sample.
let z = {[ 4, 1 ]} : float;
let s = {[ 4, 1 ]} : float;
z = x * W;
s = sigmoid_matrix(z);
This step finishes forward propagation. Actually, if values in matrix W
were correct then we would get also proper output values. Unfortunatelly
they need to adjusted by backpropagation phase.
Backpropagation
The network needs to pass several learning cycles to change random values
W set in initial phase into such which will give smallest error and
thus expected results.
Lets recall that matrix s contains output values for each input value.
Error can be calculated by subtracting each element of yT from s.
Of course we keep these values in a matrix.
let err = {[ 4, 1 ]} : float;
err = yT - s;
Now we should correct weights in matrix W so that values for each input
will lead to smallest error. For that sigmoid derivation is used. One may
easily check that first derivative of function s = 1.0 / (1.0 + exp(-x)) is
sD = s * (1 - s). First derivative multiplied by error (or function
gradient) lets to move towards minimum of a function. This method is known
as gradient descent. Please note that we want to correct values in W by
subtracting error. Also we want to move in gradient's opposite direction.
Thus plus sign in the equation. To summarize backpropagation equation is
W = W + xT * err * sD.
All calculation are done for each input value at once. Matrix of input values
is given by transpose of matrix T. To multiply values by their
corresponding elements matrix Hadamard multiplication is used.
Value 1 is replaced by matrix with all elements initialized to 1.
let sD = {[ 4, 1 ]} : float;
let one = {[ 4, 1 ]} : float;
sD = Hadamard_matrix(s, one - s);
W = W + xT * Hadamard_matrix(err, sD)
Learning cycles are executed using loop over forward and backpropagation phases.
let i = 0;
for (i = 0; i < 1000; i = i + 1)
Listing
func nn() -> int
{
let W = {[ 3, 1 ]} : float;
let one = {[ 4, 1 ]} : float;
let rand = randomize(165);
one_matrix(one);
rand_matrix(W, rand);
let z = {[ 4, 1 ]} : float;
let s = {[ 4, 1 ]} : float;
let i = 0;
for (i = 0; i < 1000; i = i + 1)
{
let x = [ [0.0f, 1.0f, 0.0f],
[1.0f, 0.0f, 0.0f],
[1.0f, 1.0f, 1.0f],
[0.0f, 0.0f, 1.0f] ] : float;
z = x * W;
s = sigmoid_matrix(z);
let y = [ [1.0f, 0.0f, 1.0f, 0.0f] ] : float;
let yT = T_matrix(y);
let err = yT - s;
let sD = Hadamard_matrix(s, one - s);
W = W + T_matrix(x) * Hadamard_matrix(err, sD)
};
z = ([[ 0.0f, 1.0f, 0.0f ]] : float) * W;
s = sigmoid_matrix(z);
print_matrix(s);
z = ([[ 0.0f, 1.0f, 0.0f ]] : float) * W;
s = sigmoid_matrix(z);
print_matrix(s);
0
}
The above code presents the whole network learning algorithm on one listing.
Beginning at the End
func main() -> int
{
nn();
}
All code in Never begins in main function. Thus we only execute function
nn inside it.
| [ X ] | y | expected |
|---|---|---|
| [ 1, 1, 1 ] | 0.96 | 1.00 |
| [ 1, 1, 0 ] | 1.00 | 1.00 |
| [ 1, 0, 1 ] | 0.00 | 0.00 |
| [ 1, 0, 0 ] | 0.05 | 0.00 |
| [ 0, 1, 1 ] | 1.00 | 1.00 |
| [ 0, 1, 0 ] | 1.00 | 1.00 |
| [ 0, 0, 1 ] | 0.05 | 0.00 |
| [ 0, 0, 0 ] | 0.50 | 0.00 |
Of course it is interesting to verify what neural network responses are. I prepared a code which outputs values for every possible input. As you may see in seven out of eight cases the network returns expected values.
Summary
The article demonstrates how Never language can be used to define a simple neural network. Also supervised neural network learning algorithm is demonstrated. I hope you liked the article and learnt something useful about neural networks, matrix algebra or Never programming language.